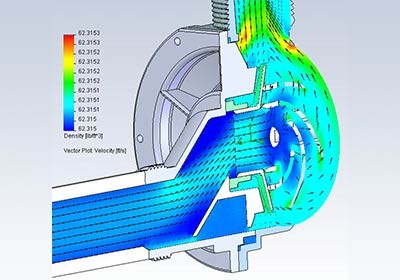
由于有限元分析在進(jìn)行前需要對(duì)網(wǎng)格進(jìn)行劃分來(lái)了解與計(jì)算機(jī)目標(biāo)的匹配程度�,因?yàn)檫@直接影響到后期有限元計(jì)算的相關(guān)質(zhì)量,雖然很多時(shí)候?qū)τ谝恍┙Y(jié)構(gòu)簡(jiǎn)單的對(duì)象可以直接使用生成法��,但是針對(duì)一些結(jié)構(gòu)復(fù)雜的對(duì)象還是要進(jìn)行相應(yīng)的計(jì)算才行��。接下來(lái)就流體有限元分析前網(wǎng)格劃分的幾種方法來(lái)做以更加詳盡化的闡釋�����。
方法一:擴(kuò)展法
網(wǎng)格劃分的常見方法就是擴(kuò)展法���,這種方法的使用頻率是相對(duì)較高的����,通常如果是曲面且形狀較為規(guī)則的話就可以采取這種方法來(lái)進(jìn)行劃分,實(shí)際劃分當(dāng)中需要結(jié)合不同的節(jié)點(diǎn)來(lái)進(jìn)行����,之后直接擴(kuò)展到平面的二維單元當(dāng)中����,這種方式所生成的網(wǎng)格質(zhì)量較高且速度也會(huì)更快,而且后期還可以生成不同的網(wǎng)格形式�����,比如說(shuō)對(duì)三維實(shí)體進(jìn)行擴(kuò)展等等可以結(jié)合實(shí)際需要對(duì)其進(jìn)行隨意調(diào)整等����。
方法二:三角形法
三角形法比較適合在一些單連通領(lǐng)域或者連通的領(lǐng)域當(dāng)中進(jìn)行使用,這種方法能夠直接對(duì)三角形進(jìn)行離散��,而且在實(shí)際的計(jì)算當(dāng)中還可以考慮到幾何圖形的特點(diǎn)��,既能夠快速的完成計(jì)算又可以很好的照顧到單元網(wǎng)格的每一個(gè)細(xì)微特征�,同時(shí)在實(shí)際使用當(dāng)中還可以對(duì)局部進(jìn)行相應(yīng)的優(yōu)化處理等等,這種方法更加適合一些復(fù)雜圖形的綜合計(jì)算����,可更好的對(duì)網(wǎng)格進(jìn)行快速有效劃分從而增加工作效率��。
事實(shí)上流體有限元分析前網(wǎng)格劃分的方法種類比較多��,實(shí)際應(yīng)用當(dāng)中需結(jié)合當(dāng)前的場(chǎng)景來(lái)選擇合適的方式����,其中比較常用的前沿法更加適合一些曲面的劃分����,比如說(shuō)四邊形或者三角形單元等等,直接通過(guò)曲面參變的方式來(lái)更換到二維空間當(dāng)中然后進(jìn)行計(jì)算即可���。