眾所周知,世界上的事物或者過程都可以進(jìn)行部分分解��,整體作為每個小不等的有機(jī)統(tǒng)一���,是具有一定的結(jié)構(gòu)的���。結(jié)構(gòu)之間互相聯(lián)系作用就讓事物的整體具有了一定的屬性和規(guī)律。結(jié)構(gòu)優(yōu)化有限元分析的原理���,正是基于這個大前提�����。這不是一個簡單的拆分和組合的關(guān)系��,是一個復(fù)雜的工藝結(jié)構(gòu)關(guān)系�����。
理論基礎(chǔ)
首先我們需要明確一個概念��,有限元的元�,是指代什么?Element即單元��,是有限元的另一常規(guī)稱呼���。在結(jié)構(gòu)分析的過程中�,結(jié)構(gòu)會被分成有限個單元�����。這就是有限元的來源���。單元之間會存在某些關(guān)系����,一般是通過Node(節(jié)點(diǎn))進(jìn)行結(jié)構(gòu)之間的連接�����。所以通過以上我們可以知道���,單元和節(jié)點(diǎn)這兩個概念就是形成有限元模型的基礎(chǔ)單位�。隨著科技的不斷發(fā)展�����,目前已經(jīng)有許許多多的工具進(jìn)行這一分析�,也被大量用在工業(yè)及理論學(xué)習(xí)上。
基本流程
對其進(jìn)行分析首先是要有限元網(wǎng)絡(luò)的離散���,然后進(jìn)行位移差值函數(shù)的選取形成位移場����。之后形成單元剛度矩陣(即變分原理)��,再合成總體剛度矩陣。引入一定的邊界條件之后就能求解線性方程得到節(jié)點(diǎn)位移數(shù)據(jù)����,根據(jù)數(shù)據(jù)得到相對應(yīng)的應(yīng)力、應(yīng)變(內(nèi)力)�。為了讓有限元的模型更加有效地逼近實(shí)際體,需要考慮的還包括了單元的形狀和劃分節(jié)點(diǎn)網(wǎng)絡(luò)的方案(如數(shù)目����、位置、自由度等等)���。
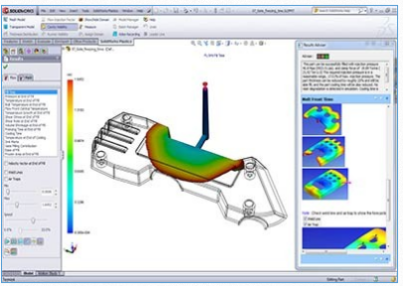
Partly determines the whole(部分決定整體)�����,在產(chǎn)品設(shè)計中��,結(jié)構(gòu)優(yōu)化有限元分析是進(jìn)行多方位考慮�����,對結(jié)構(gòu)進(jìn)行校核和優(yōu)化的必要手段���,這一方法在工業(yè)運(yùn)用中較為廣泛���。經(jīng)過這一設(shè)計���,產(chǎn)品更加具有全面性和可靠性�,也擁有更加高的市場競爭力���。